The open star cluster NGC 1960 (Messier 36) in the auriga constellation
D. Linhart, P. Stinner, D. Stock, M. Urban
Astronomy team, Kopernikus Gymnasium, Pirzenthalerstraße 43, D-57537 Wissen
1.Introduction
During the years 2001 and 2002 the astronomy team of the Kopernikus-Gymnasium
at Wissen (Germany) performed the project "Colour magnitude diagrams of
open galactic star clusters". The projects aims were the creation of colour
magnitude diagrams (CMDs) of eight open clusters as well as the evaluation with
respect to distances and ages of the clusters. We were introduced into fundamental
techniques for detection and analysis of astronomical and physical experimental
values and resulting data. We got basic and solid insights in methods of astronomical
science. We have learned much about the enormous importance of CMDs resp. HRDs
(Hertzsprung-Russel-Diagrams) for the evaluation of stellar evolution. -
For decades the observatory of the Geschwister Scholl Realschule at Betzdorf
(50°48`N; 7°53`E) had been vacant. In 2001 it was reactivated by our team.
We there installed an 8" Schmidt Cassegrain telescope (Celestron C8) with
a computer controlled CCD camera. In addition we built a computer network for
internet access and to control the CCD camera and the autoguider.
CCD images in B and V were taken with a ST6 CCD camera. They became corrected
by darkframe and flatfield. Our schoolmate Fabian Bieler produced the special
software WinStarFinder, by means of which the images were analysed. Our aparatus
was calibrated using reference stars out of the WEBDA database [8].
The project was one of the German contributions to "Physics on Stage 2"
(April 02nd 06th 2002) in Noordwijk, the Netherlands. It was presented on April
the 27th 2002 at the open day of the astronomical institutes of Bonn university.
While performing the project we "felt in love" with the cluster NGC
1960. The experiments went on without any difficulties, the produced CMD shows
a nice main sequence. Therefore we choosed NGC 1960 as the object of our contribution
to the ESO competition CATCH A STAR.
2. Galactic open star clusters
Open star clusters are nondense accumulations of stars with irregular shape.
They contain from about 10 to about 1000 stellar objects. Open star clusters
are concentrated in the plain of our milky way system. Therefore they also are
called galactic star clusters. The number of such nondense accumulations of
stars in our galaxis is estimated to be about 15 000. Most of these clusters
have diameters between 2 and 6 pc. All the stars of the same cluster were born
at nearly the same time by the collapse of a rather dense cloud of interstellar
dust. "Nearly the same time" means, that the time of the birth of
the stars is extremely short compared with the age of the clusters as it can
be observed nowadays [2; 16]. The most famous open clusters are the plejades
and the hyades in the taurus constellation, and the praesepe in the cancer constellation.
The auriga constellation is well known for the great number of open clusters,
e.g. NGC 2281, NGC 1912 (M38), NGC 2099 (37) and our favourite cluster NGC 1960
(M36).
The most important properties of open clusters were explored by using colour
magnitude diagrams. We will describe this way of working in chapter 4. There
we will analyse distance and age of NGC 1960 by using a self created CMD.
3. Properties of the cluster NGC 1960 (M36) from literature
NGC 1960 (M36) is located at RA=5h36m, DEC=+34°8. It is belonging to the auriga
constellation, which is circumpolar. From our location in the middle of Germany
it may be seen all over the year. Best opportunities for observing NGC 1960
exist in January and February, when the cluster culminates in the evening.
Its diameter is about d=10 [7]. Morphologically, NGC 1960 is dominated by
a number of bright (V≤11 mag) stars, whereas the total stellar density
is only marginally enhanced compared to the surrounding field. For the first
time CCD photometric studies were performed by Sanner et al. [10]. Sanner et
al. determined the distance of the cluster to 1318(120)pc and its age to be
16(+10/-5) millions of years.
The fact that NGC 1960 is a rather young cluster is the reason for the existence
of the former mentioned bright stars, which have absolute magnitudes of up to
about -2mag. With increasing age the stars one by one will leave the main sequence
in the CMD starting with the brightest stars. At first they will change to red
giants, later to white dwarfs. The cluster will become darker and less brilliant
[5].
4. Our own investigations of properties of NGC 1960
4.1 Images of NGC 1960
The astronomy team of the Kopernikus Gymnasium at Wissen (Germany) exists since 1993. During this time many photos of numerous objects in the sky were taken using conventional films. And so were the following, except the RGB composite (inset 4 in figure 1):

Figure 1: NGC 1960 and its surrounding in the sky; all images taken by the ASTRO-AG, Kopernikus-Gymnasium, D-57537 Wissen
Data:
Inset 1:The sky in the winter (18. Jan. 1999, location: Gebhardshain (D); Scotch Come 400, f=20mm;
f/D=2.8; exp. time = 4min; tracking by self-made mount)
Inset 2: The auriga constellation (25. Jan. 1998, location: Gebhardshain (D); Scotch Crome 400, f= 50mm;
f/D=3.4; exp. time = 7min, tracking by self-made mount)
Inset 3: Auriga region with the open clusters M38 and M36 (27. Oct. 1997, location: Gebhardshain (D); Kodak P1600X/P3, f=200mm;
f/D=4, exp. time = 12min)
Inset 4: CCD RGB composite of NGC 1960, 09. Dec. 2001, location: Betzdorf (D);
f= 900mm; f/D=4.5,
4.2 Creation of the CMD of NGC 1960
The creation of an open clusters CMD needs CCD images in B (blue) and V (visual/green). They were taken by us in our school observatory at the Geschwister-Scholl-Realschule in D-57518 Betzdorf (geographical coordinates: see chapter 1). The optic used was an 8" Celestron C8 telescope with a focal reducer (f=900mm, f/D=4.5). A ST6 CCD camera and the software CCDOPS [13] were used for the production of the CCD images. The tracking was done by a ST4 autoguider. The B images were taken with Schott filters BG12 (blue) and KG5 (infrared exclusion filter), the V images with VG9 (green) and KG5. The transmission functions of these filter combinations [11] are shown in figure 2. The exposure times were 300 seconds in B and in V.
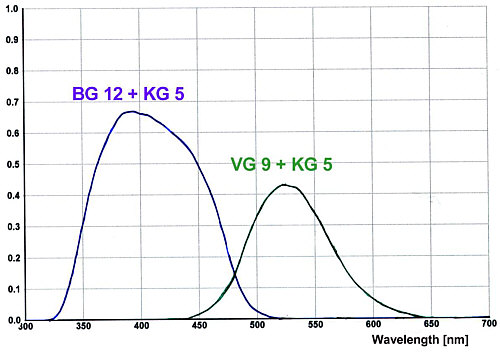
Figure 2: Transmission functions of our B and V filter combinations
The special software WinStarFinder (author: Fabian Bieler,
der.fabe@gmx.net)
was created to construct and evaluate our CMDs. For every star that is represented
in both the V and the B images of NGC 1960 WinStarFinder calculated the numbers
NB and NV of electrons in the concerned pixels as linear
values for the preliminary magnitudes of the stars.
Using the B and V values of reference stars of the WEBDA database [8] and a
minimisation routine of the ROOT software package [9] WinStarFinder at first
calculated calibration functions by means of which the preliminary magnitudes
NB and NV are converted into the apparent magnitudes B
and V and the colour indices B-V of all stars. Since B and V are logarithmic
values for the brightness of stars the colour index B-V describes the gradient
of the Planck function between the filter ranges B and V [3]. Simplified B-V
describes the colour of a star, whereas B-V increases from blue stars up to
red stars.
In the colour magnitude diagram every star is represented by a dot, whose coordinates
are B-V and V. The so gained CMD of NGC 1960 is shown in figure 3.
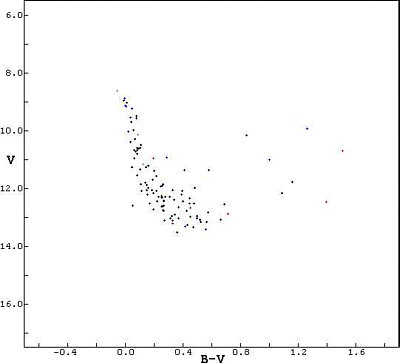
Figure 3: Self produced colour magnitude diagram of NGC 1960
4.3 Determination of some properties of NGC 1960 out of our CMD
4.3.1 Correction of the data by reddening and interstellar extinction
Before calculating NGC 1960`s distance and age the CMD data had to be corrected
by reddening and interstellar extinction.
The reason for reddening is scattering of light at small interstellar dust particles.
The shortwave blue light partially is scattered out of the light path [4; 14].
The so caused reddening is described by the colour excess E(B-V).
The corrected colour indices (B-V)0 arise from the not corrected
values B-V (see 4.2) by:
(B V)0 = (B V) E(B V) [4; 14] (1)
Scattering at interstellar dust also causes an attenuation of light that is proportional to the value of reddening. The so corrected apparent visual magnitude V0 is:
V0 = V AV ≈ V0 3 E(B V) [4: 14] (2)
All the following calculations had to be performed by using the corrected values
V0 and (B V)0. The required value of the colour excesses
E(B-V) is given in [6] to be
E(B-V) (NGC 1960) = 0.24.
4.3.2 Calculation of the distance of the cluster
Figure 4 shows the zero age main sequence (ZAMS) [6] in an CMD of an open cluster in the standard distance 10pc. Stars at that standard distance have per definitionem the absolute visual magnitude MV.
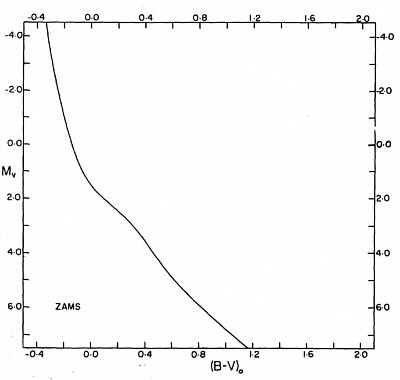
Figure 4: The ZAMS (zero age main sequence) [6]
The absolute visual magnitude MV of an arbitrary star, its corrected
apparent visual magnitude V0, and its distance d (in pc) are related
by the following equation [4]:
V0 - MV = 5 log d 5 (3)
V0 MV is called the "distance modulus". If the ZAMS in figure 4 is shifted by the distance modulus V0 - MV it will be at the same place as the main sequence in the considered CMD is (see figure 5). Note that for determination of the distances modulus the CMD has to be corrected by reddening and interstellar extinction. That means the upper axis ((B-V)0 in figure 5) must be considered concerning the colour excess. Furthermore the apparent V magnitude has to be corrected by the interstellar extinction according to equation (2).
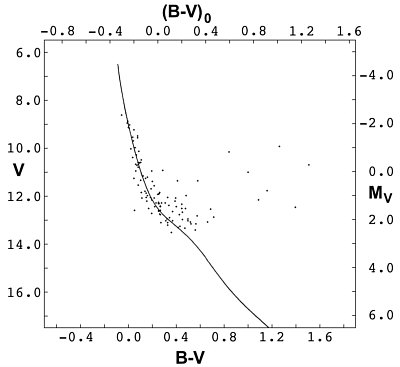
Figure 5: The CMD of NGC 1960 with the fitted ZAMS. Note the shift of the (B-V)0-axis relative to the (B-V)-axis by the colour excess E(B-V)=0.24.
From figure 5 the distance modulus of NGC 1960(M36) is determined to be V0-MV = 10.4(0.35). So the distance of NGC 1960 calculated by equation (3) is
d = 1220(200)pc = 4000(650) light years
4.3.3 Calculation of the ages of the cluster NGC 1960
The V magnitude of the brightest stars in the CMD of an open cluster is called the "turn off point" V* of the main sequence. The theory of stellar evolution gives a relationship between the age T of an open cluster and the corrected (!) V magnitude MV* of the stars at the turn off points of the main sequences in the clusters` CMD [15]:
T = (2,5 108yr) exp(MV*/0,99mag) for MV* < 1mag, or
T = (3,2 108yr) exp(MV*/1,60mag) for MV* > 0mag (4)
For NGC 1960 figure 5 gives MV* = 8,85 AV (V0-MV) ≈ -2,27(0,35) and the age to be:
T = 27(10) millions of years.)
4.3.4 Comparison with recently published values
Sanner et al. [10] recently published up to date values of NGC 1960: Their
distance is d = 1318(120)pc, their age T = 16(-5/+10) millions of years.
Although our distance value 1220(200)pc has got a larger error band the result
of Sanner et al. is situated within this error band.
The measured resp. calculated ages of Sanner et al. and of ourselves are compatible
within the error bands.
Notice that our experimental potentialities do not allow to correct our CMDs
by field stars. Our CMDs therefore are contaminated by such stars that are to
be seen on the line of vision to the cluster although they are no members of
the cluster.
Since the transmission functions of our filter combinations (see figure 2) slightly
differ from those in the standard UBV system [12] another experimental error
occurs.
5. Comparison of NGC 1960 and NGC 2281
NGC 2281 is another open cluster in the auriga constellation. Like NGC 1960 it was an object of our CCD photometry project in 2001/2002.
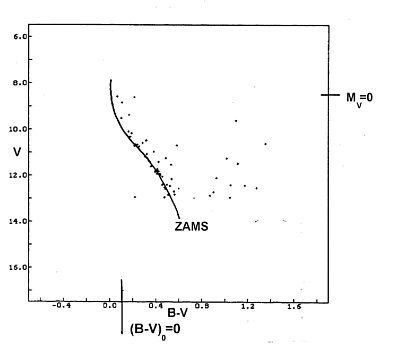
Figure 6: Self produced colour magnitude diagram of NGC 2281 with the fitted ZAMS.
In the same way as described for NGC 1960 in chapter 4.3 we fitted the ZAMS
to the CMD of NGC 2281 (see figure 6). With E(B-V)=0.10 [6] we obtained
the distance modulus V-MV = 8.4(0.3) resp. the corrected value V0-MV
= 8.1(0.3) so that the distance of NGC 2281 is 420(60)pc. This is only about
a third of NGC 1960`s distance. Hagen [6] gives the value V-MV=8.8
(without error bands) for NGC 2281`s distance modulus. This corresponds to V0-MV=8.5
and to a distance of 500pc.
In figure 6 the turn off point of the main sequence is situated at about V*=8.8(0.3).
With V0-MV=8.1(0.3) and E(B-V)=0.1 the age
of NGC 2281 may be calculated by equation (4) (see chapter 4.3.3) to be 400(200)
millions of years. Alter et al. [1] give the value 500 millions of years. NGC
2281 is much older than NGC 1960. Many members of NGC 2281 already have left
the main sequence (fig. 6).
6. Literature
[1] Alter, G., Ruprecht, J., Vanysek, J.: Catalogue of
Star Clusters and Associations, Budapest 1970
[2] de Boer, K. et al.: Astronomie Gymnasiale Oberstufe Grundstudium, Berlin
2001
[3] de Boer, K.S.: Das Hertzsprung-Russell-Diagramm und
das Maß der Sterne, Astronomie + Raumfahrt 38 (6/2001), S. 18-22
[4] Götz, W.: Die offenen Sternhaufen unserer Galaxis,
Leipzig 1989
[5] Gondolatsch, F., Steinacker, S,. Zimmermann, O.: Astronomie Grundkurs,
Stuttgart 1990
[6] Hagen, G.L.: An Atlas of Open Cluster Colour Magnitude
Diagrams, Toronto 1970
[7] Lynga, G.: Catalog of open cluster data, 5th edition, 1987
[8] Mermilliod, J.-C.: WEBDA Database of Open Clusters,
obswww.unige.ch/webda
[9] Root Software Package: root.cern.ch
[10] Sanner, J., Altmann, M., Brunzendorf, J., Geffert, M.: Photometric
and kinematic studies of open star clusters, Astronomy and Astrophysics 357,
471-483 (2000)
[11] Schott Glas: Katalog Optische Filter Glasfilter, Version
1.1.D, Mainz 1998
[12] Unsöld, A., Baschek, B.: Der neue Kosmos, Berlin,
Heidelberg 1999
[13] www.sbig.com
[14] Zimmermann, O.: Der galaktische Sternhaufen NGC 7789,
Astronomie + Raumfahrt 38 (6/2001), S. 4445
[15] Zimmermann, O.: private communication
[16] Zimmermann, H., Weigert, A.: Lexikon der Astronomie, Heidelberg, Berlin,
1999
7. Practical exercise: Determination of NGC 1960`s distance and its age by
means of our self created CMD
The practical exercise needs the CMD of NGC 1960 (see figure 3) as well as the ZAMS (see figure 4). Figure 5 (CMD of NGC 1960 with fitted ZAMS) should not be given!
Practical exercise:
Determination of NGC 1960`s distance and age out of a colour magnitude diagram, that was created by the astronomy team of the Kopernikus-Gymnasium in D-57537 Wissen
Materials:
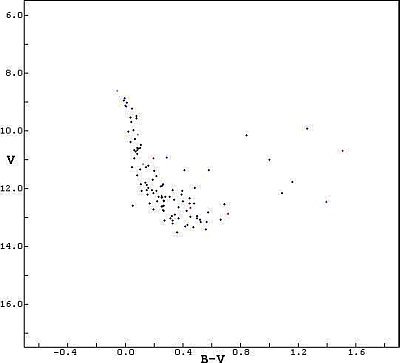
Figure 1: Colour magnitude diagram of NGC 1960
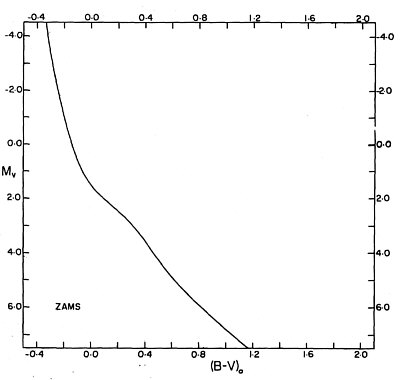
Figure 2: ZAMS (zero age main sequence) of a star cluster
See the two figures 1 and 2. Figure 1 shows the colour magnitude diagram (CMD) of the open star cluster NGC 1960 as it was created by the astronomy team of the Kopernikus-Gymnasium in D-57537 Wissen based on CCD images in B and V. The images were taken on 09.Dec. 2001 at the observatory of the Geschwister-Scholl-Realschule at D-57518 Betzdorf with a C8 telescope (f=900mm;f/D=4.5) and an ST6 CCD camera.
Meaning of the dots in the CMD:
Every dot in fig. 1 represents a star in the open cluster NGC 1960. B and V are the apparent B and V magnitudes, B-V is the so called "colour index" that represents the colour of a star. B-V increases from blue stars up to red stars.
Correction by reddening an interstellar extinction:
On the way through the galaxis the light becomes reddened and attenuated caused by scattering at small interstellar dust particles. The shortwave blue light is partially scattered out of the light path. The so caused reddening is described by the colour excess E(B-V). So the corrected colour indices (B-V)0 arises from the not corrected values B-V by:
(B V)0 = (B V) E(B V) [4; 14] (1)
Scattering at interstellar dust also causes an attenuation of light that is proportional to the value of reddening. The so corrected apparent visual magnitude V0 is:
V0 = V AV ≈ V0 3 E(B V) [4: 14] (2)
All the following calculations in this exercise must be performed by using the corrected values V0 and (B V)0. The required value of the colour excesses E(B-V) is E(B-V) = 0.24 for the open cluster NGC 1960.
Determination of the distance of NGC 1960
Figure 2 shows the zero age main sequence (ZAMS) in a CMD of an open cluster
in the standard distance 10pc. Stars at that standard distance have per definitionem
the absolute visual magnitude MV.
The absolute visual magnitude MV of an arbitrary star, its corrected
apparent visual magnitude V0, and its distance d (in pc) are related
by the following equation
V0 - MV = 5 log d 5 (3)
V0 MV is called the "distance modulus". If
the ZAMS in figure 2 is shifted by the distance modulus V0 - MV
it will be at the same place as the main sequence in the considered CMD is.
Note that for determination of the distance modulus the CMD first has to be
corrected by reddening. That means the ZAMS must be shifted to the right by
the amount of E(B-V)=0.24. Then you should shift the ZAMS diagram
up or down until the ZAMS curve fits the main sequence in the CMD. Then the
zero point of the MV-axis on the right corresponds to a certain value
of the V-axis in the CMD on the left.
This V value is the (not corrected) distance modulus V-MV. Now the
distance modulus may be corrected by interstellar extinction by
means of equation
(2). At last equation (3) gives the distance of the open cluster NGC 1960.
Determination of the age of NGC 1960
The V magnitude of the brightest stars in the CMD of an open cluster is called the "turn off point" V* of the main sequence. Brighter stars, that means stars with smaller V magnitude already have left the main sequence. They have changed to red giants or even to white dwarfs. The theory of stellar evolution gives a relationship between the age T of an open cluster and the corrected (!) absolute (!) V magnitude MV* of the stars at the turn off point of the main sequences of the clusters` CMD:
T = (2,5 108yr) exp(MV*/0,99mag) for MV* < 1mag (4)
T = (3,2 108yr) exp(MV*/1,60mag) für MV* > 0mag (5)
Now you are able to determine V* from the CMD in figure 1 and calculate MV* using your distance modulus and the equations (2) and (3).The value of MV* determines, whether equation (4) or equation (5) is the right one to calculate the age NGC 1960.